Geometric Computing
Geometric Computingis one of the most coolest courses I've taken in EPFL. This course covers mathematical concepts and efficient numerical methods for geometric computing. It is a project-based course, where we develop and implement algorithms to simulate and optimize 2D and 3D geometric models with an emphasis towards computational design for digital fabrication.
There are mainly 3 projects in this course: Make it stand, Elastic Material Fabriction, and Asymptotic Grid Shell Design.
1. Make it stand
The goal of this project is to optimize the shape of an object so that it stands in a desired pose under gravity by implementing a simplified 2D variant of the 2013 SIGGRAPH Paper "Make It Stand" by Prévost et al.
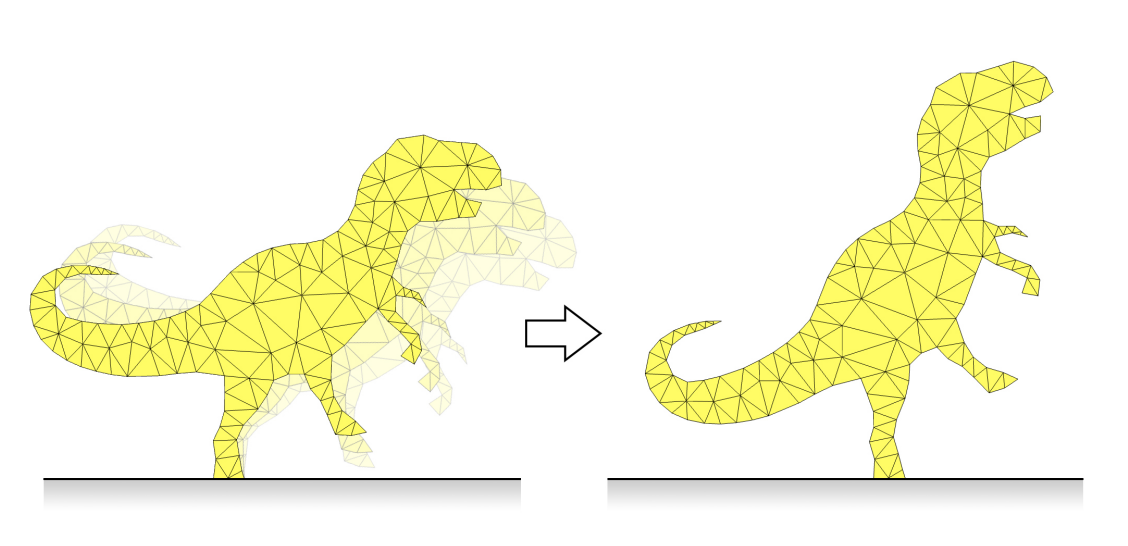
We implemented BFGS algorithm to find the optimized the shape. The objective function is composed by the equilibrium energy, the shape energy, and the constrain of the face area. Therefore, the deformed shape can best preserve the original shape, meaning that it looks like the original shape, but it can stand without falling down.
Aside from the example shape provided by the course for testing, we were encourged to try some other shape as well. Here is my final result (gray: original shape, yellow: optimized shape):
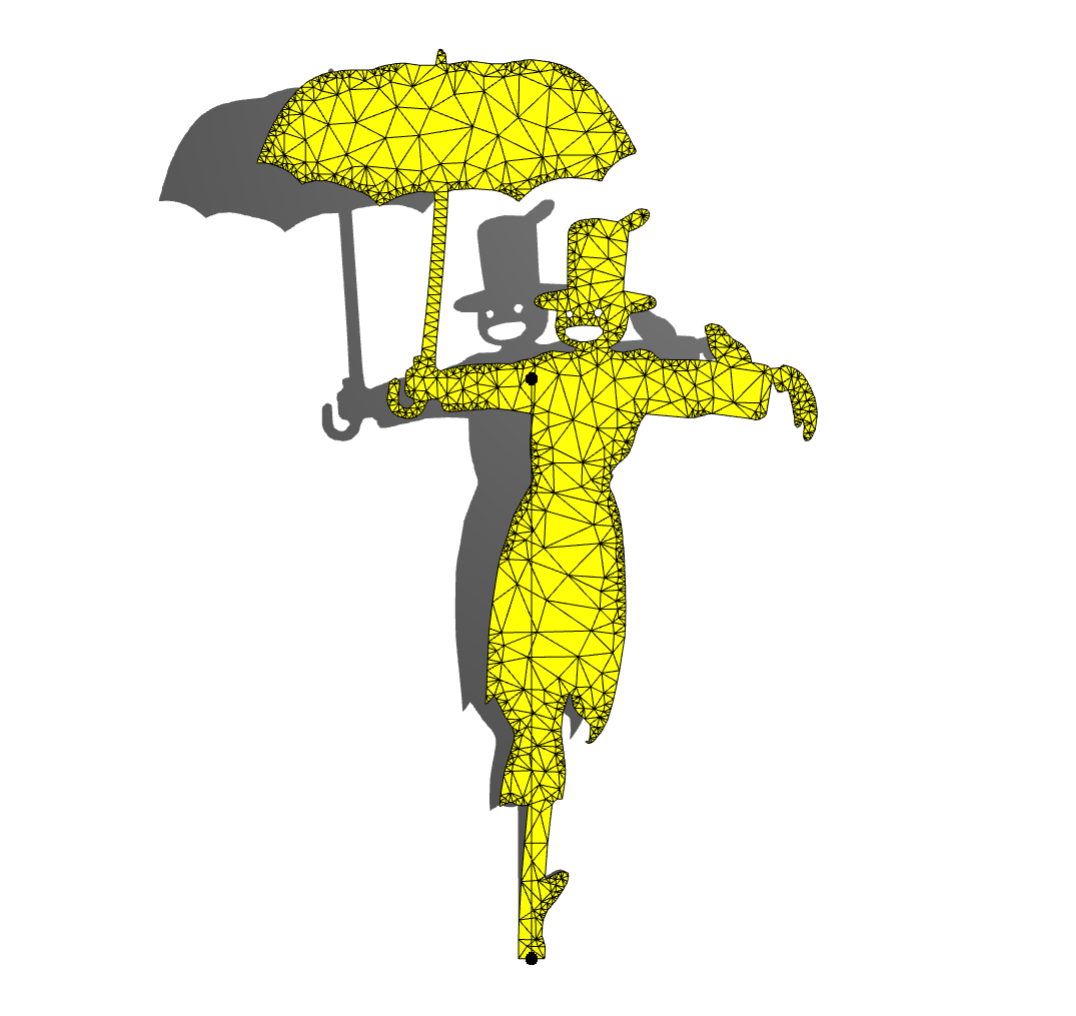
2. Inverse Design of Elastic Solids

If we want to manufacture the model using elastic material and fabricate the desired shape directly, gravity would deform it and result in an unwanted result, as shown on the left in the picture. Therefore, to ensure that the final shape is what we desire despite the effects of gravity, we must determine the rest shape that will deform into the desired shape under the gravity forces.
The concept of this project is similar to the previous "make it stand", but with a more complex optimization target. In addition to BFGS, we also implemented the Newton-Conjugate Gradient to find the optimized shape, which reduces the computation time dramatically and sometimes even finds a better result.
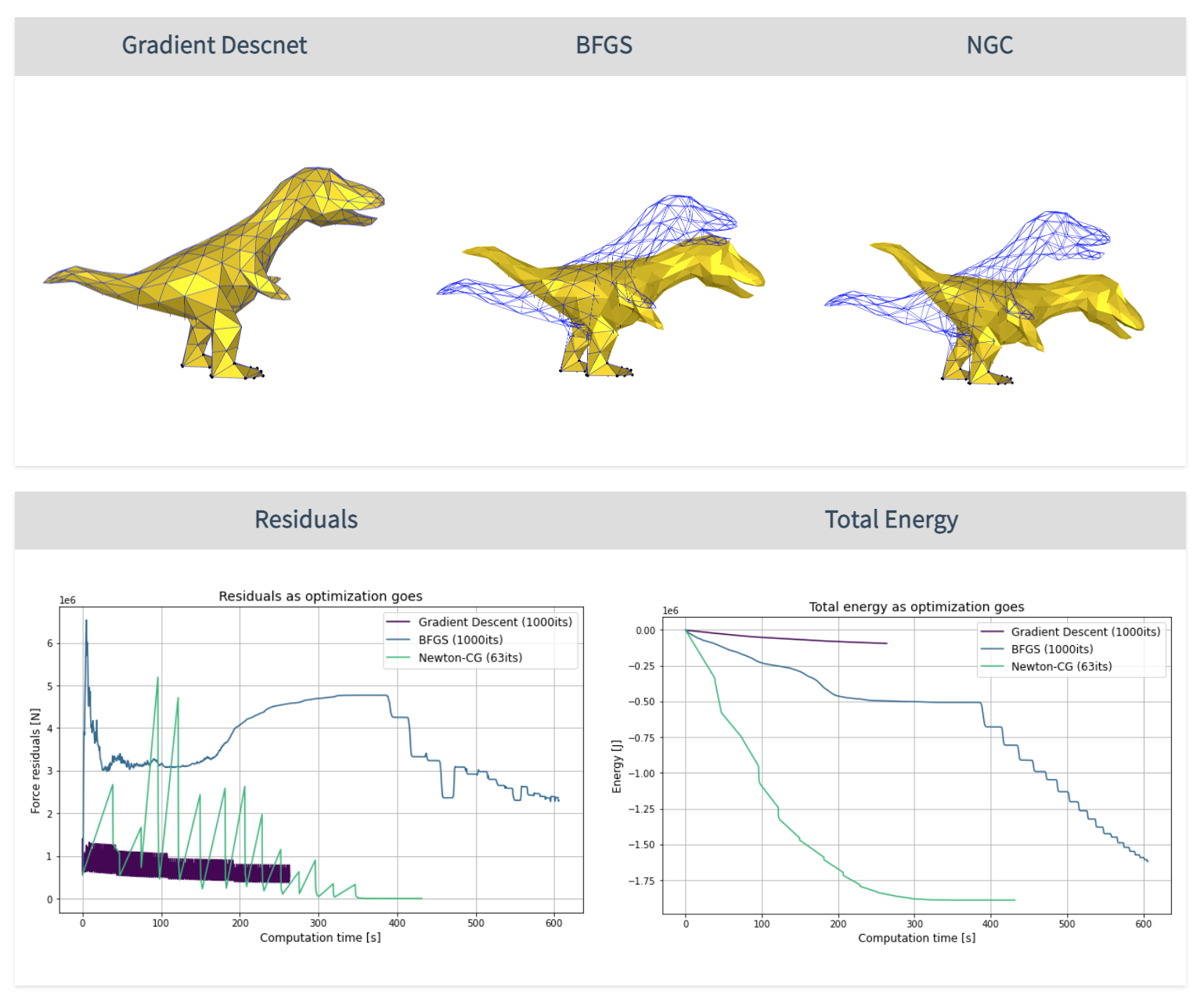
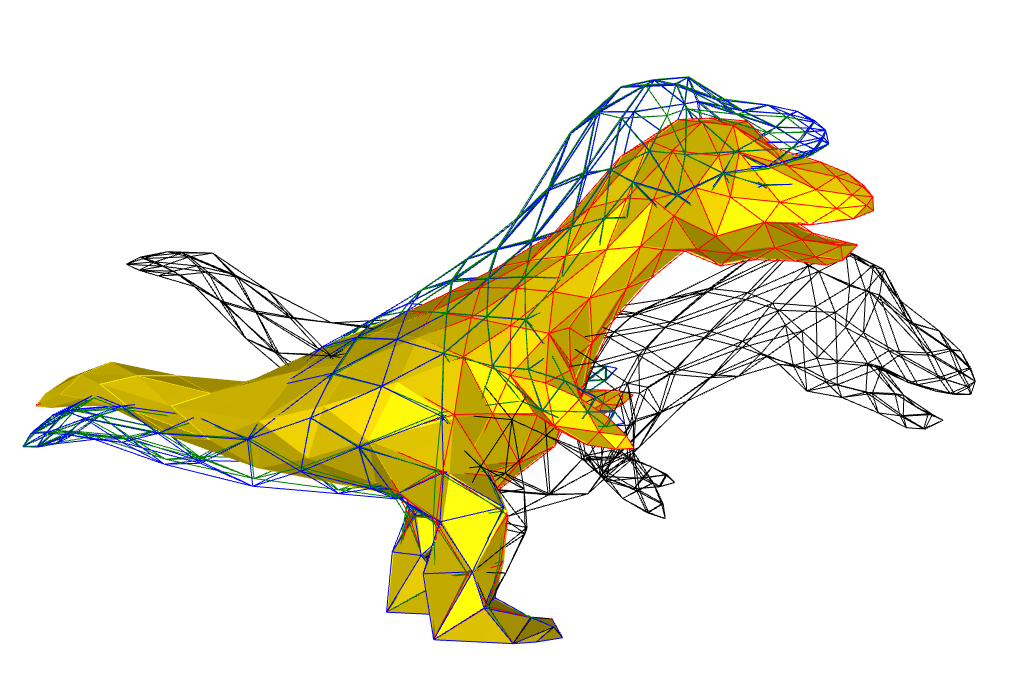
The final result is shown in the picture below. Originally, if we fabricate the desired shape (red) directly, we would get an unwanted shape(black). Now with inverse design, we can find the rest shape of the elastic model for fabrication (blue / green), and the deformed shape (yellow) would be similar to the desired shape (red).
3. Asymptotic Grid Shell Design


The asymptotic curve comes with a special property that is beneficial for digital fabrication. The structure formed by a grid of asymptotic curves can be fabricated from straight and flat elements by laser-cutter, making the manufacture process easier and minimizing the packing size.
The minimal surface, on the other hand, is an ideal structure to be form by an asymptotic grid. Since the minimal surface has zero mean curvature at all points, the asymptotic curve can be found at every given point on the surface. Therefore, we can fabricate the minimal surface with an approximate uniformally distributed asymptotic grid.
The goal of this project is to find the minimal surface with a given border, and with the user input of the desired point on the surface, form the corresponding asymptotic grid. The result is shown in the picture below.

At the end of the course, we also voted for some shape created by the students and laser cut the stripes and assemble them together.




